DISCLAIMER
The present benchmark was conducted on 2025-06-11 on a Macbook Pro M4
(12-core CPU, 16-core GPU, 24GB RAM). Results will vary
depending on the hardware. The benchmarks are intended to provide a
general idea of the performance differences between the fio
package and other implementations, but they should not be considered
definitive. The performance of the functions may also vary depending on
the specific data used and the context in which the functions are
applied.
Introduction
This vignette presents a benchmarking analysis comparing the
performance of functions from the fio package with
equivalent base R functions. The fio package provides a set
of functions for input-output analysis, a method used in economics to
analyze the interdependencies between different sectors of an
economy.
In this document, we will focus on two key functions: the technical coefficients matrix calculation and the Leontief inverse matrix calculation. These functions are fundamental to input-output analysis, and their performance can significantly impact the speed of larger analyses.
Our benchmarking tests, which involve running these functions
repeatedely in simulated datasets, show that the fio
package functions are faster than other implementations. This improved
performance can make a substantial difference in larger analyses, making
the fio package a valuable tool for input-output analysis
in R.
The tests were run on a simulated matrix, and each test was repeated 100 times to account for variability. Please note that the results of this benchmarking analysis are dependent on the specific test datasets used and the hardware on which the algorithms were run. Therefore, the results should be interpreted in the context of these specific conditions.
Technical coefficients matrix
The technical coefficients matrix calculation, a key and initial step
in input-output analysis, was tested using the
compute_tech_coeff() function from the fio
package, equivalent functions from the leontief package,
and a base R implementation. It consists on dividing each
element of intermediate transactions matrix by the correspondent
element of total production vector1.
# set seed
set.seed(100)
# Base R function
tech_coeff_r <- function(intermediate_transactions, total_production) {
tech_coeff_matrix <- intermediate_transactions %*% diag(1 / as.vector(total_production))
return(tech_coeff_matrix)
}
# benchmark
benchmark_a <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
bench::mark(
fio = fio:::compute_tech_coeff(intermediate_transactions, total_production),
`Base R` = tech_coeff_r(intermediate_transactions, total_production),
leontief = leontief::input_requirement(intermediate_transactions, total_production),
iterations = 100
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
#> Warning: Some expressions had a GC in every iteration; so filtering is
#> disabled.
print(benchmark_a)
#> # A tibble: 12 × 14
#> expression matrix_dim min median `itr/sec` mem_alloc `gc/sec` n_itr
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl> <int>
#> 1 fio 100 49.57µs 81.41µs 11381. 861.83KB 0 100
#> 2 Base R 100 59.61µs 78.72µs 11191. 190.65KB 0 100
#> 3 leontief 100 131.45µs 161.95µs 6175. 706.38KB 62.4 99
#> 4 fio 500 445.67µs 625.95µs 1562. 1.91MB 65.1 96
#> 5 Base R 500 940.38µs 1.27ms 722. 3.82MB 80.2 90
#> 6 leontief 500 1.73ms 2.11ms 464. 16.29MB 691. 41
#> 7 fio 1000 1.83ms 2.38ms 405. 7.63MB 83.0 83
#> 8 Base R 1000 6.56ms 7.88ms 125. 15.27MB 70.1 64
#> 9 leontief 1000 8.46ms 8.6ms 116. 65MB 9131. 2
#> 10 fio 2000 9.56ms 10.89ms 87.9 30.52MB 12.3 100
#> 11 Base R 2000 45.27ms 52.44ms 18.8 61.05MB 6.38 100
#> 12 leontief 2000 39.91ms 62.49ms 16.4 259.7MB 44.6 100
#> # ℹ 6 more variables: n_gc <dbl>, total_time <bch:tm>, result <list>,
#> # memory <list>, time <list>, gc <list>
# plot
ggplot2::autoplot(benchmark_a)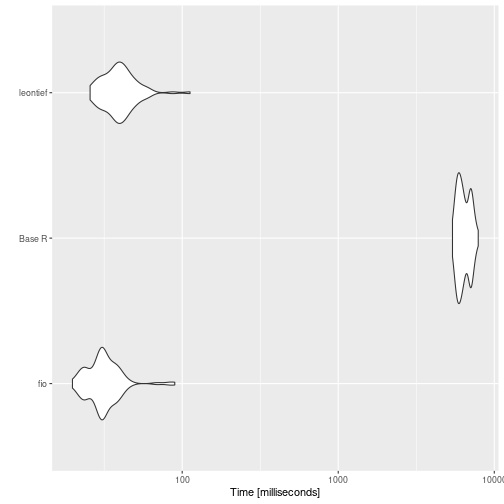
is faster.
Leontief inverse matrix
When we’re talking about inverting a there’s a lot more work involved. Leontief matrix () is obtained from subtracting the technical coefficients matrix () from the identity matrix (), therefore it has no null rows or columns.
It allows for solving the linear system through LU decomposition, which is a more efficient method than the direct inverse matrix calculation.
# base R function
leontief_inverse_r <- function(technical_coefficients_matrix) {
dim <- nrow(technical_coefficients_matrix)
leontief_inverse_matrix <- solve(diag(dim) - technical_coefficients_matrix)
return(leontief_inverse_matrix)
}
# benchmark
benchmark_b <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
iom_fio$compute_tech_coeff()
technical_coefficients_matrix <- iom_fio$technical_coefficients_matrix
bench::mark(
fio = fio:::compute_leontief_inverse(technical_coefficients_matrix),
`Base R` = leontief_inverse_r(technical_coefficients_matrix),
leontief = leontief::leontief_inverse(technical_coefficients_matrix),
iterations = 100,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
#> Warning: Some expressions had a GC in every iteration; so filtering is
#> disabled.
print(benchmark_b)
#> # A tibble: 12 × 14
#> expression matrix_dim min median `itr/sec` mem_alloc `gc/sec` n_itr
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl> <int>
#> 1 fio 100 138.58µs 339.4µs 2410. 158.51KB 0 100
#> 2 Base R 100 254.04µs 356.86µs 2765. 413.27KB 0 100
#> 3 leontief 100 270.72µs 363.4µs 2837. 402.57KB 0 100
#> 4 fio 500 4.83ms 5.78ms 172. 3.81MB 3.51 98
#> 5 Base R 500 3.96ms 4.27ms 230. 9.55MB 20.0 92
#> 6 leontief 500 3.99ms 4.26ms 231. 9.55MB 20.1 92
#> 7 fio 1000 24.13ms 27.31ms 36.6 15.26MB 3.62 91
#> 8 Base R 1000 16.67ms 17.36ms 56.8 38.18MB 16.0 78
#> 9 leontief 1000 15.96ms 17.3ms 57.3 38.18MB 16.2 78
#> 10 fio 2000 129.76ms 136.91ms 7.26 61.03MB 1.45 100
#> 11 Base R 2000 85.67ms 89.92ms 10.9 152.66MB 11.1 100
#> 12 leontief 2000 85.94ms 90.43ms 10.8 152.66MB 10.8 100
#> # ℹ 6 more variables: n_gc <dbl>, total_time <bch:tm>, result <list>,
#> # memory <list>, time <list>, gc <list>
# plot
ggplot2::autoplot(benchmark_b)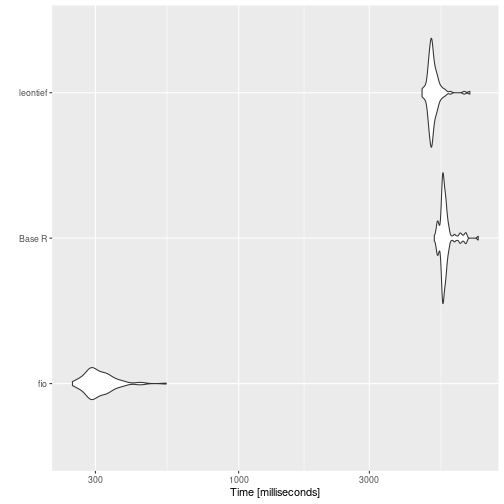
{fio} is incredibly faster.
Sensitivity of dispersion coefficients of variation
To represent linkage-based functions performance, we compute benchmark for sensitivity of dispersion coefficients of variation.
# base R function
sensitivity_r <- function(B) {
n <- nrow(B)
SL = rowSums(B)
ML = SL / n
(((1 / (n - 1)) * (colSums((B - ML) ** 2))) ** 0.5) / ML
}
# benchmark
benchmark_c <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
iom_fio$compute_tech_coeff()$compute_leontief_inverse()
leontief_inverse_matrix <- iom_fio$leontief_inverse_matrix
bench::mark(
fio = fio:::compute_sensitivity_dispersion_cv(leontief_inverse_matrix),
`Base R` = sensitivity_r(leontief_inverse_matrix),
leontief = leontief::sensitivity_dispersion_cv(leontief_inverse_matrix),
iterations = 100,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
#> Warning: Some expressions had a GC in every iteration; so filtering is
#> disabled.
print(benchmark_c)
#> # A tibble: 12 × 14
#> expression matrix_dim min median `itr/sec` mem_alloc `gc/sec` n_itr
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl> <int>
#> 1 fio 100 130.05µs 193.19µs 4449. 81.23KB 0 100
#> 2 Base R 100 21.48µs 25.07µs 19494. 81.48KB 0 100
#> 3 leontief 100 512.99µs 544.77µs 1826. 745.38KB 18.4 99
#> 4 fio 500 445.34µs 592.8µs 1652. 1.91MB 0 100
#> 5 Base R 500 468.18µs 551.22µs 1808. 1.92MB 0 100
#> 6 leontief 500 10.46ms 11.03ms 90.3 17.31MB 6.79 93
#> 7 fio 1000 1.49ms 1.68ms 581. 7.64MB 0 100
#> 8 Base R 1000 1.8ms 2.11ms 474. 7.66MB 14.6 97
#> 9 leontief 1000 61.18ms 62.3ms 16.0 68.94MB 9.42 63
#> 10 fio 2000 4.94ms 5.16ms 192. 30.53MB 0 100
#> 11 Base R 2000 8.14ms 8.27ms 115. 30.58MB 21.9 100
#> 12 leontief 2000 286.46ms 301.14ms 3.24 275.22MB 4.60 100
#> # ℹ 6 more variables: n_gc <dbl>, total_time <bch:tm>, result <list>,
#> # memory <list>, time <list>, gc <list>
ggplot2::autoplot(benchmark_c)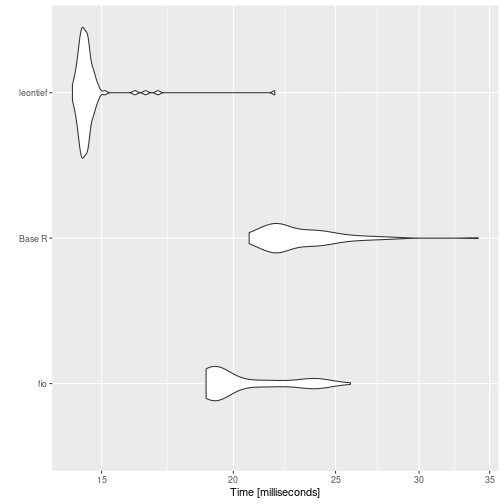
{fio} again faster.
Field of influence
Since field of influence involves computing Leontief inverse matrix for each element of technical coefficients matrix after an increment, it can be demanding for high dimensional matrices. Here, we evaluate benchmark for base R function and {fio}, since there’s no similiar function in {leontief}. For brevity, we cut dimensions to 100 and repetitions to 10.
# base R function
field_influence_r <- function(A, B, ee = 0.001) {
n = nrow(A)
I = diag(n)
E = matrix(0, ncol = n, nrow = n)
SI = matrix(0, ncol = n, nrow = n)
for (i in 1:n) {
for (j in 1:n) {
E[i, j] = ee
AE = A + E
BE = solve(I - AE)
FE = (BE - B) / ee
FEq = FE * FE
S = sum(FEq)
SI[i, j] = S
E[i, j] = 0
}
}
return(SI) # Added return statement
}
# benchmark
benchmark_d <- bench::press(
matrix_dim = c(30, 60, 100),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio_reduced <- fio::iom$new(
"iom_reduced",
intermediate_transactions,
total_production
)$compute_tech_coeff()$compute_leontief_inverse()
bench::mark(
fio = fio:::compute_field_influence(
iom_fio_reduced$technical_coefficients_matrix,
iom_fio_reduced$leontief_inverse_matrix,
0.001
),
`Base R` = field_influence_r(
iom_fio_reduced$technical_coefficients_matrix,
iom_fio_reduced$leontief_inverse_matrix
),
iterations = 10,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 30
#> 2 60
#> Warning: Some expressions had a GC in every iteration; so filtering is
#> disabled.
#> 3 100
#> Warning: Some expressions had a GC in every iteration; so filtering is
#> disabled.
print(benchmark_d)
#> # A tibble: 6 × 14
#> expression matrix_dim min median `itr/sec` mem_alloc `gc/sec` n_itr
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl> <int>
#> 1 fio 30 5.47ms 5.51ms 181. 16.67KB 0 10
#> 2 Base R 30 23.76ms 24.17ms 41.3 44.52MB 10.3 8
#> 3 fio 60 111.41ms 111.72ms 8.95 56.34KB 0 10
#> 4 Base R 60 718.27ms 726.39ms 1.37 701.2MB 2.75 10
#> 5 fio 100 3.6s 5.07s 0.203 156.34KB 0 10
#> 6 Base R 100 4.24s 4.26s 0.234 5.25GB 3.83 10
#> # ℹ 6 more variables: n_gc <dbl>, total_time <bch:tm>, result <list>,
#> # memory <list>, time <list>, gc <list>
ggplot2::autoplot(benchmark_d)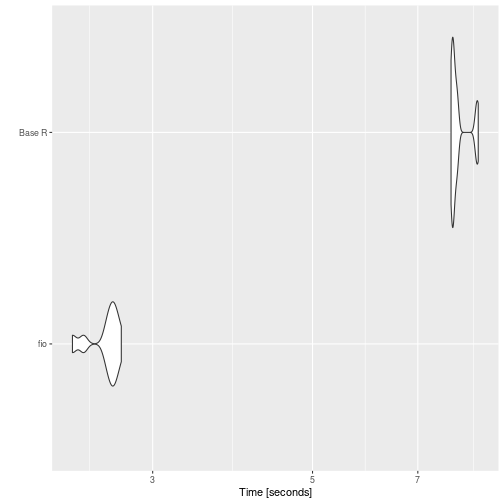
{fio} faster.
Or in a equivalent way, multiplying intermediate transactions matrix by a diagonal matrix constructed from total production vector.↩︎