DISCLAIMER
The present benchmark was conducted on 2025-06-17 on a Macbook Pro M4
(12-core CPU, 16-core GPU, 24GB RAM). Results will vary
depending on the hardware. These benchmarks aim to provide a general
idea of the performance differences between the fio package
and other implementations but should not be considered definitive. The
performance of the functions may also vary depending on the specific
data used and the context in which they are applied.
Introduction
This vignette presents a benchmarking analysis comparing the
performance of functions from the fio package with
equivalent base R functions and functions from other packages. The
fio package provides a set of functions for input-output
analysis, a method used in economics to analyze the interdependencies
between different sectors of an economy.
Our benchmarking tests show that fio package functions
are generally faster than other implementations. This improved
performance can make a substantial difference in larger analyses, making
the fio package a valuable tool for input-output analysis
in R.
The tests were run on simulated square matrices, with dimensions ranging from 100x100 up to 2000x2000, and each test was repeated at least 50 times to account for variability. Please note that the results of this benchmarking analysis depend on the specific test datasets used and the hardware on which the algorithms were run. Therefore, the results should be interpreted in the context of these specific conditions.
Technical coefficients matrix
The technical coefficients matrix calculation, a key and initial step
in input-output analysis, was tested using the
compute_tech_coeff() function from the fio
package, equivalent functions from the leontief package,
and a base R implementation. It consists of dividing each
element of the intermediate transactions matrix by the corresponding
element of the total production vector1.
Results shows that {fio} is generally faster than the other two implementations, especially for larger matrices (≥500x500).
# set seed
set.seed(100)
# Base R function
tech_coeff_r <- function(intermediate_transactions, total_production) {
tech_coeff_matrix <- intermediate_transactions %*% diag(1 / as.vector(total_production))
return(tech_coeff_matrix)
}
# benchmark
benchmark_a <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
bench::mark(
fio = fio:::compute_tech_coeff(intermediate_transactions, total_production),
`Base R` = tech_coeff_r(intermediate_transactions, total_production),
leontief = leontief::input_requirement(intermediate_transactions, total_production),
iterations = 100
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
print(benchmark_a)
#> # A tibble: 10 × 9
#> expression matrix_dim min median mem_alloc `gc/sec` n_itr n_gc total_time
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <bch:byt> <dbl> <int> <dbl> <bch:tm>
#> 1 fio 100 48.17µs 72µs 861.83KB 0 100 0 7.95ms
#> 2 Base R 100 52.03µs 82.78µs 190.65KB 0 100 0 9.26ms
#> 3 leontief 100 138.13µs 152.93µs 706.38KB 64.8 99 1 15.43ms
#> 4 fio 500 433.7µs 646.57µs 1.91MB 80.6 95 5 62.04ms
#> 5 Base R 500 941.89µs 1.21ms 3.82MB 86.4 90 10 115.81ms
#> 6 leontief 500 1.84ms 2.13ms 16.29MB 826. 38 67 81.07ms
#> 7 fio 1000 1.73ms 2.67ms 7.63MB 63.9 86 14 219.15ms
#> 8 Base R 1000 6.54ms 7.85ms 15.27MB 67.5 65 35 518.57ms
#> 9 leontief 1000 8.84ms 8.84ms 65MB 16847. 1 149 8.84ms
#> 10 fio 2000 9.02ms 12.94ms 30.52MB 40.5 67 33 815.73ms
#> 11 Base R 2000 46.12ms 51.36ms 61.05MB 41.0 32 68 1.66s
#> 12 leontief 2000 36.67ms 36.67ms 259.7MB 5400. 1 198 36.67ms
# plot
ggplot2::autoplot(benchmark_a)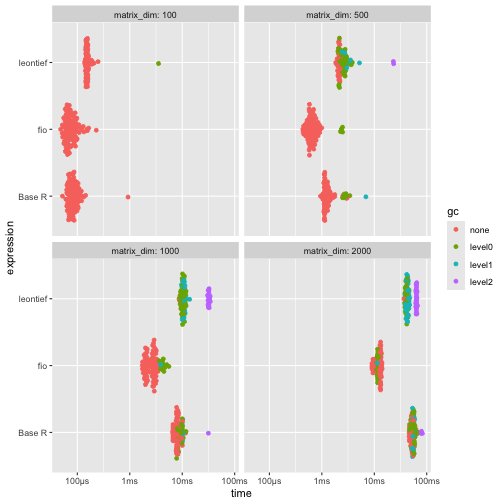
For larger matrices (≥500x500), {fio} is generally faster.
Leontief inverse matrix
The Leontief matrix () is obtained by subtracting the technical coefficients matrix () from the identity matrix (); therefore, it has no null rows or columns. This allows for solving the linear system through LU decomposition, which is a more efficient method than direct inverse matrix calculation.
Results shows that {fio} is slightly slower.
# base R function
leontief_inverse_r <- function(technical_coefficients_matrix) {
dim <- nrow(technical_coefficients_matrix)
leontief_inverse_matrix <- solve(diag(dim) - technical_coefficients_matrix)
return(leontief_inverse_matrix)
}
# benchmark
benchmark_b <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
iom_fio$compute_tech_coeff()
technical_coefficients_matrix <- iom_fio$technical_coefficients_matrix
bench::mark(
fio = fio:::compute_leontief_inverse(technical_coefficients_matrix),
`Base R` = leontief_inverse_r(technical_coefficients_matrix),
leontief = leontief::leontief_inverse(technical_coefficients_matrix),
iterations = 100,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
print(benchmark_b)
#> # A tibble: 12 × 9
#> expression matrix_dim min median mem_alloc `gc/sec` n_itr n_gc total_time
#> 1 fio 100 136.65µs 442.43µs 158.51KB 0 100 0 77.88ms
#> 2 Base R 100 279.87µs 336.47µs 413.27KB 0 100 0 34.86ms
#> 3 leontief 100 219.72µs 330.58µs 402.57KB 0 100 0 30.46ms
#> 4 fio 500 4.76ms 5.88ms 3.81MB 1.67 99 1 597.14ms
#> 5 Base R 500 3.93ms 4.22ms 9.55MB 12.2 95 5 411.44ms
#> 6 leontief 500 3.98ms 4.21ms 9.55MB 9.55 96 4 419.01ms
#> 7 fio 1000 22.27ms 26.02ms 15.26MB 0.781 98 2 2.56s
#> 8 Base R 1000 16.08ms 17.46ms 38.18MB 11.6 83 17 1.47s
#> 9 leontief 1000 16.47ms 17.43ms 38.18MB 12.5 82 18 1.44s
#> 10 fio 2000 130.66ms 138.6ms 61.03MB 1.48 83 17 11.51s
#> 11 Base R 2000 85.16ms 88.54ms 152.66MB 97.4 11 95 975.6ms
#> 12 leontief 2000 84.71ms 88.36ms 152.66MB 63.9 17 96 1.5s
# plot
ggplot2::autoplot(benchmark_b)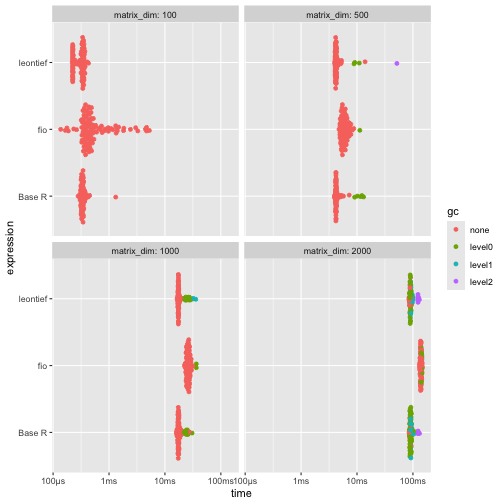
{fio} is slightly slower.
Sensitivity of dispersion coefficients of variation
To evaluate the performance of linkage-based functions, we benchmarked the sensitivity of dispersion coefficients of variation.
Results shows that {fio} is substantially faster than {leontief} across all tested dimensions. Compared to Base R, {fio} is faster for matrices 1000x1000 and larger.
# base R function
sensitivity_r <- function(B) {
n <- nrow(B)
SL = rowSums(B)
ML = SL / n
(((1 / (n - 1)) * (colSums((B - ML) ** 2))) ** 0.5) / ML
}
# benchmark
benchmark_c <- bench::press(
matrix_dim = c(100, 500, 1000, 2000),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio <- fio::iom$new("iom", intermediate_transactions, total_production)
iom_fio$compute_tech_coeff()$compute_leontief_inverse()
leontief_inverse_matrix <- iom_fio$leontief_inverse_matrix
bench::mark(
fio = fio:::compute_sensitivity_dispersion_cv(leontief_inverse_matrix),
`Base R` = sensitivity_r(leontief_inverse_matrix),
leontief = leontief::sensitivity_dispersion_cv(leontief_inverse_matrix),
iterations = 100,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 100
#> 2 500
#> 3 1000
#> 4 2000
print(benchmark_c)
#> # A tibble: 12 × 9
#> expression matrix_dim min median mem_alloc `gc/sec` n_itr n_gc total_time
#> 1 fio 100 113.41µs 196.9µs 81.23KB 0 100 0 20.14ms
#> 2 Base R 100 22.67µs 25.62µs 81.48KB 0 100 0 5.52ms
#> 3 leontief 100 528.61µs 543.99µs 745.38KB 18.5 99 1 54.19ms
#> 4 fio 500 451.74µs 639.99µs 1.91MB 0 100 0 64.3ms
#> 5 Base R 500 522.87µs 548.95µs 1.92MB 0 100 0 55.39ms
#> 6 leontief 500 10.35ms 11.09ms 17.31MB 4.74 95 5 1.05s
#> 7 fio 1000 1.47ms 1.66ms 7.64MB 0 100 0 168.68ms
#> 8 Base R 1000 1.8ms 2.11ms 7.66MB 9.64 98 2 207.37ms
#> 9 leontief 1000 61.2ms 62.76ms 68.94MB 3.73 81 19 5.09s
#> 10 fio 2000 5ms 5.26ms 30.53MB 0 100 0 533.11ms
#> 11 Base R 2000 8.25ms 8.41ms 30.58MB 11.8 91 9 765.12ms
#> 12 leontief 2000 290.27ms 290.27ms 275.22MB 575. 1 167 290.27ms
# plot
ggplot2::autoplot(benchmark_c)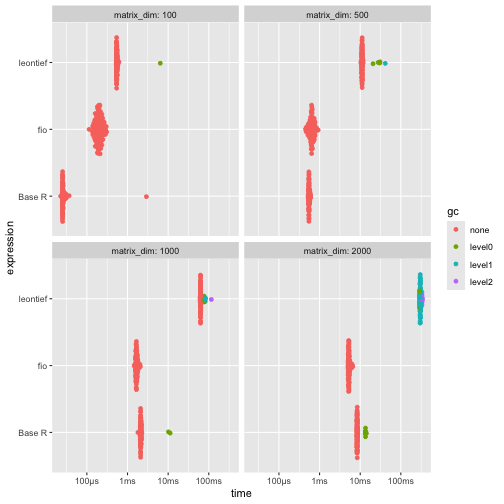
{fio} is substantially faster than {leontief} across all tested dimensions. Compared to Base R, {fio} is faster for matrices 1000x1000 and larger.
Field of influence
Since computing the field of influence involves calculating the Leontief inverse matrix for each element of the technical coefficients matrix after an increment, it can be demanding for high-dimensional matrices. Here, we benchmark the base R function and fio, as there is no similar function in leontief. For brevity, we limited the matrix dimensions to 200x200 and the number of repetitions to 20.
Results shows that {fio} is considerably faster for smaller matrices, but slightly slower for larger ones.
# base R function
field_influence_r <- function(A, B, ee = 0.001) {
n = nrow(A)
I = diag(n)
E = matrix(0, ncol = n, nrow = n)
SI = matrix(0, ncol = n, nrow = n)
for (i in 1:n) {
for (j in 1:n) {
E[i, j] = ee
AE = A + E
BE = solve(I - AE)
FE = (BE - B) / ee
FEq = FE * FE
S = sum(FEq)
SI[i, j] = S
E[i, j] = 0
}
}
return(SI) # Added return statement
}
# benchmark
benchmark_d <- bench::press(
matrix_dim = c(30, 60, 100, 200),
{
intermediate_transactions <- matrix(
as.double(sample(1:1000, matrix_dim^2, replace = TRUE)),
nrow = matrix_dim,
ncol = matrix_dim
)
total_production <- matrix(
as.double(sample(4000000:6000000, matrix_dim, replace = TRUE)),
nrow = 1,
ncol = matrix_dim
)
iom_fio_reduced <- fio::iom$new(
"iom_reduced",
intermediate_transactions,
total_production
)$compute_tech_coeff()$compute_leontief_inverse()
bench::mark(
fio = fio:::compute_field_influence(
iom_fio_reduced$technical_coefficients_matrix,
iom_fio_reduced$leontief_inverse_matrix,
0.001
),
`Base R` = field_influence_r(
iom_fio_reduced$technical_coefficients_matrix,
iom_fio_reduced$leontief_inverse_matrix
),
iterations = 20,
check = FALSE
)
}
)
#> Running with:
#> matrix_dim
#> 1 30
#> 2 60
#> Warning: Some expressions had a GC in every iteration; so filtering is disabled.
#> 3 100
#> Warning: Some expressions had a GC in every iteration; so filtering is disabled.
#> 4 200
#> Warning: Some expressions had a GC in every iteration; so filtering is disabled.
print(benchmark_d)
#> # A tibble: 8 × 9
#> expression matrix_dim min median mem_alloc `gc/sec` n_itr n_gc total_time
#> <bch:expr> <dbl> <bch:tm> <bch:tm> <bch:byt> <dbl> <int> <dbl> <bch:tm>
#> 1 fio 30 5.43ms 5.48ms 16.67KB 0 20 0 109.52ms
#> 2 Base R 30 24.1ms 24.48ms 44.52MB 10.2 16 4 393.39ms
#> 3 fio 60 111.31ms 112.34ms 56.34KB 0 20 0 2.25s
#> 4 Base R 60 659.28ms 677.31ms 701.2MB 4.14 20 56 13.53s
#> 5 fio 100 3.18s 5.14s 156.34KB 0 20 0 1.75m
#> 6 Base R 100 3.84s 3.97s 5.25GB 4.71 20 376 1.33m
#> 7 fio 200 41.43s 48.95s 625.09KB 0 20 0 16.52m
#> 8 Base R 200 44.46s 44.85s 83.73GB 11.3 20 10379 15.32m
ggplot2::autoplot(benchmark_d)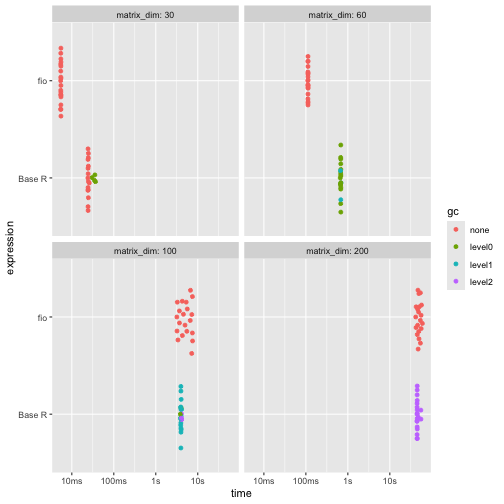
{fio} is faster for smaller matrices.
Or equivalently, multiplying the intermediate transactions matrix by a diagonal matrix constructed from the total production vector.↩︎